En 2004 el Institut Catogràfic de Catalunya decide dar el paso final hacia la consecución de una línea de producción cartográfica totalmente digital y se adquiere mediante concurso una cámara fotogramétrica digital. El modelo elegido fue una Digital Mapping Camera (DMC) desarrollada y comercializada por ZEISS/INTERGRAPH (Z/I). Posteriormente, se incorporó una segunda cámara de este mismo modelo a finales de 2005. Estas cámaras presentan, frente a las analógicas, una mejor resolución para una misma altura de vuelo. A cambio, la relación base / altura es mejor en el caso analógico, debido a la diferencia de formato de las imágenes.
El necesario cambio en los parámetros de configuración de un vuelo tras la incorporación de estas cámaras al flujo productivo del Instituto acrecienta la necesidad de disponer de un método para determinar de forma objetiva la calidad de un vuelo fotogramétrico. Esta herramienta ha de ser también aplicable a vuelos analógicos de cara a definir un criterio único para todos los proyectos de la casa y a sintonizar los nuevos parámetros de vuelo manteniendo intacta la calidad del producto resultante.
Un parámetro importante de cara a determinar la calidad de un vuelo es, precisamente, la resolución efectiva de cada uno de los fotogramas que lo integran.
2. Metodología
A lo largo de todo el proyecto se ha trabajado con imágenes sintéticas para realizar pruebas y un patrón estrella de Siemens (vea Figura 1) de 144 sectores i 6 cm. de diámetro que se ha escaneado mediante hardware de varios fabricantes. Se han obtenido imágenes del patrón con:
Escáner: Delta1, resolución 16 micras.
Escáner: Tdscan, resolución 14 micras.
Posteriormente se generan imágenes sintéticas del patrón en correspondencia con las que se han obtenido mediante el escaneo.

Figura 1: Patrón estrella de Siemens
2.1 Construcción de la Función de Transferencia de la Modulación (MTF)
Una caracterización de la resolución afín a los parámetros ópticos habituales nos viene dada por la función MTF, cuya información resume el comportamiento global del sistema. Por otra parte, con intención de atribuir al sistema una medida concreta de resolución en magnitud píxel, se considera la medida FWHM (anchura a mitad del máximo de la función) de la LSF. Por ese motivo, se implementan ambos métodos, fundamentales hoy en día, para la caracterización del poder de resolución de un sistema formador de imagen.
2.1.1 Algoritmo 1. Cálculo de de Función de transferencia del Contraste
Se implementa una herramienta software con el objetivo de calcular una aproximación discreta de la función MTF. Esta herramienta está completamente adaptada y automatizada para patrones estrella de Siemens. La detección del centro del patrón se lleva a cabo mediante la implementación de la transformada de Hough. El usuario debe introducir los parámetros correspondientes al número de sectores que tiene el patrón y su radio máximo en magnitud píxel, además de las coordenadas de un punto situado en un contorno. El esquema que sigue el algoritmo es el siguiente:
1) Para el círculo de radio máximo se localizan los píxeles de las bisectrices de cada sector, como en el método descrito por Honkavaara et al. [1,2]
2) Se almacenan los valores digitales correspondientes a los sectores “blancos” y se promedian. Se sigue el mismo procedimiento para los valores digitales correspondientes a los sectores “negros”, y se emplean dichos promedios en la fórmula que define el contraste:
| C = | MAX − MIN |
| MAX + MIN |
3) Se calcula el factor de transferencia del contraste como el cociente entre el contraste de la imagen y el contraste objeto, asumiendo éste como el valor de contraste obtenido para las frecuencias espaciales más bajas.
4) Se disminuye el radio en una unidad píxel y se iteran los mismos cálculos.
Esta parte del algoritmo proporciona la Función de Transferencia del Contraste, CTF. Cabe notar que la CTF será decreciente y con valor máximo igual a 1 para la frecuencia más baja.
La CTF se transforma en la MTF mediante series numéricas de conversión de Coltman [2]. La función MTF será utilizada con la finalidad de comparar el poder de resolución de los distintos sistemas que se sometan a examen y nos proporcionará una representación completa de la pérdida de contraste del sistema para cada una de las frecuencias en las que hemos descompuesto el objeto.
2.1.2 Algoritmo 2. Construcción de la Función de dispersión del borde (ESF)
Se implementa una herramienta software cuyo objetivo es dar una medida de resolución de la imagen en magnitud píxel. Esencialmente, el programa procesa una región de interés que contendrá un solo contorno y realiza un ajuste mínimo-cuadrático sobre la función bidimensional del borde, como en el método descrito por Blonski [3,4], que modelizamos como una función de tipo sigmoide
| f ( j, i) =P4 + | |
| 1 + e − P3 ⋅( i⋅cos P1 P5 +j ⋅sin P5 − P2 ) |
(1)
Pk (sumatorio) ℜ, k =1,…,5 .
El ajuste mínimo-cuadrático proporciona valores para los cinco parámetros y esta función es derivada para obtener la LSF. Consideramos como medida de resolución la medida FWHM sobre la LSF.
En el caso de utilizar el software con patrones de Siemens, se ha automatizado el procedimiento. Los parámetros de entrada son únicamente las coordenadas del centro de la estrella y las coordenadas de un punto contenido en un contorno. Mediante estos datos se generan automáticamente las regiones de interés de forma trapezoidal y se calcula una medida de resolución para cada una de ellas.
La aplicación de la Transformada de Fourier sobre la LSF obtenida nos proporciona una MTF que nos permitirá validar la consistencia de ambos métodos. [5]
2.2 Consistencia del método
La consistencia del método se ha comprobado a través de la implementación del algoritmo de la Transformada rápida de Fourier (Fast Fourier Transform, FFT), y se ha verificado que el módulo de la transformada de Fourier de la función LSF obtenida mediante el ajuste de la sigmoide coincide, en efecto, con la función MTF obtenida a través del algoritmo de construcción de la CTF (vea Figura 2).
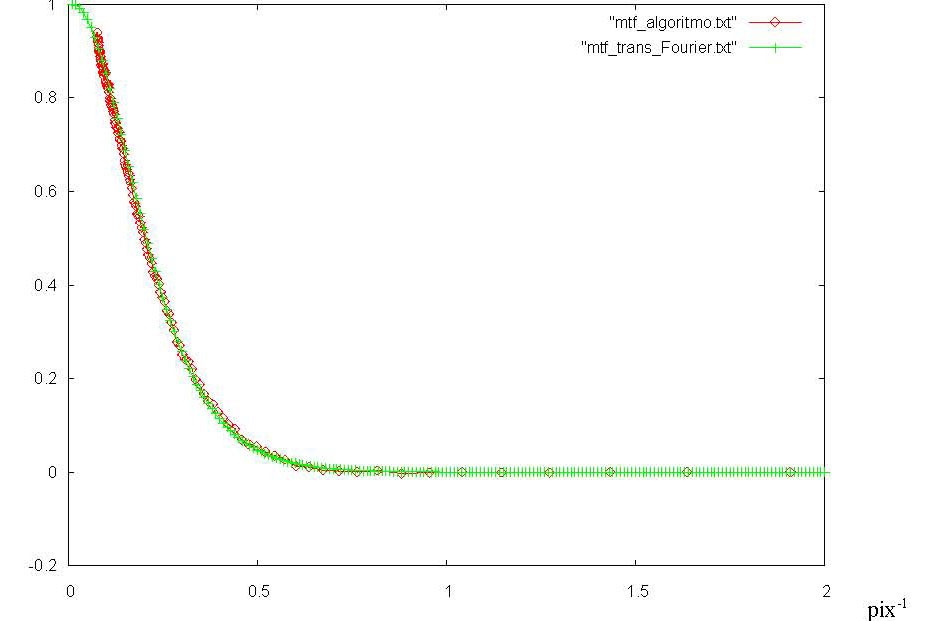
Figura 2: Comparación entre la MTF obtenida mediante el algoritmo 1(gráfica roja) y la MTF calculada como el módulo de la transformada de Fourier de la LSF obtenida mediante el algoritmo 2 (gráfica verde). Dicho ejemplo corresponde a la imagen capturada con cámara analógica y posteriormente escaneada a una resolución de 7 micras (vea Figura 10).
2. Resultados
2.1 Resultados obtenidos con imágenes sintéticas
Las pruebas sobre las imágenes sintéticas muestran resultados muy estables para ambos métodos. Aplicamos ambos algoritmos a cada uno de los patrones sintéticos y los resultados que se obtienen son la CTF y la MTF (Figura 3), y una medida de resolución para cada transición contenida en el patrón (Figura 4), respectivamente.
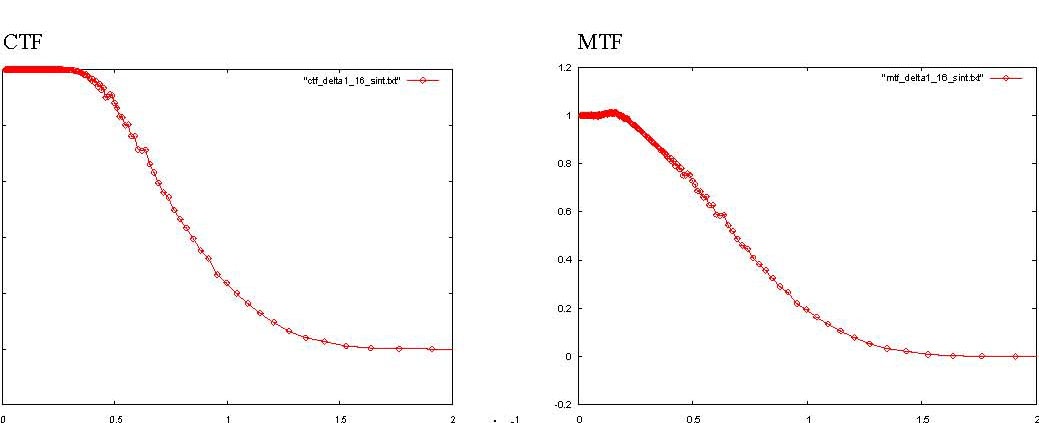
Figura 3: resultados generados por el algoritmo 1. Izquierda: función CTF calculada con imagen. Derecha: función MTF correspondiente.
La imagen sintética que se menciona en la figura 3 es la que se genera como pareja de la imagen resultante de escanear el patrón con Delta1 a 16 micras. Es interesante observar que la función CTF es constante e igual a 1 para las bajas frecuencias. Este resultado manifiesta de forma evidente que las frecuencias bajas (correspondientes al detalle tosco) sufren una degradación mínima del contraste, si es que llegan a sufrir reducción, avalando así nuestra decisión de asociar éste al contraste del objeto.
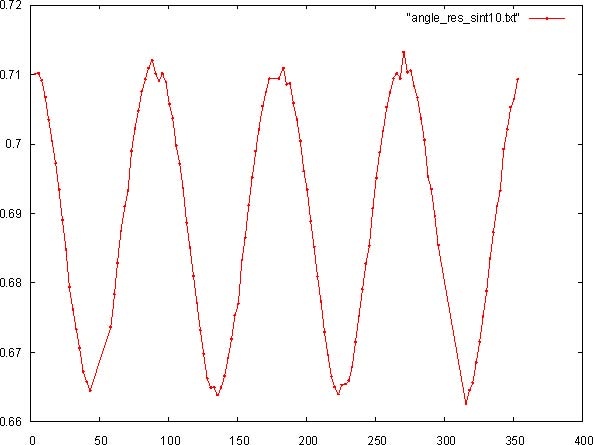
El algoritmo 2 aplicado sobre la misma imagen sintética proporciona 144 resultados de resolución, uno para cada contorno, asociado a su posición angular (vea Figura 4).
resolución (píxeles)
ángulo (grados)
Figura 4: resultados obtenidos mediante el algoritmo 2 sobre una estrella de Siemens sintética. La gráfica muestra la variación de los valores de resolución en función de la variación angular
de los contornos.
Los valores máximo y mínimo son 0,66 píxeles y 0,71 píxeles respectivamente, correspondientes a los ángulos 43,11 y 270,61. La amplitud es 0,05 píxeles. La resolución promedio es 0,69 píxeles. Los resultados para el resto de imágenes sintéticas son exactamente los mismos. Incluso modelizando nuestra función de contorno por una función de error en lugar de una función sigmoide, se mantiene la misma estructura sinusoidal de la gráfica y la misma amplitud.
2.2 Resultados obtenidos con imágenes reales
Se llevan a cabo las mismas pruebas con las imágenes reales, escaneadas mediante hardware de distintos fabricantes. Los resultados, en magnitud píxel, se presentan en forma de tabla (vea Tabla 1). En este caso, es preciso señalar que las gráficas que relacionan la resolución con la variación angular del contorno, no tienen forma sinusoidal, puesto que la diferencia de resolución entre el sentido de barrido del escáner y el perpendicular es mucho mayor que la diferencia encontrada en imágenes sintéticas.
| Imagen | Resolución media (píxel) |
Resolución media absoluta (micras) |
Valor máx. resolución (píxel) | Valor mín. resolución (píxel) | Ángulo resolución máxima | Ángulo resolución mínima | Amplitud (píxel) | Amplitud (micras) |
| Tdscan 14 micras | 1,03 | 14,48 | 1,10 | 0,69 | 99,18 | 181,68 | 0,41 | 5,74 |
| Delta1 16 micras | 1,02 | 16,44 | 1,26 | 0,78 | 98,14 | 5,67 | 0,48 | 7,68 |
Tabla 1. Resultados de resolución según diversos parámetros sometidos a estudio
3.3 Resultados obtenidos con imágenes aéreas (DMC)
Se han aplicado también ambos algoritmos sobre cuatro imágenes aéreas capturadas con la DMC del Instituto sobre un patrón estrella de Siemens pintado sobre lona de 100 m2 de superficie (vea Figuras 5, 6, 7 y 8)


Figuras 5, 6 ,7 y 8: Imágenes aéreas del patrón estrella de Siemens pintado sobre lona.
Los resultados MTF se han generado mediante la estrella de Siemens de 72 sectores (vea Figura 9), mientras que las medidas de resolución que proporciona el algoritmo 2 se han obtenido midiendo sobre el otro patrón (un cuarto de estrella de Siemens que tendría 22 sectores), puesto que las regiones de interés tienen un tamaño más adecuado.
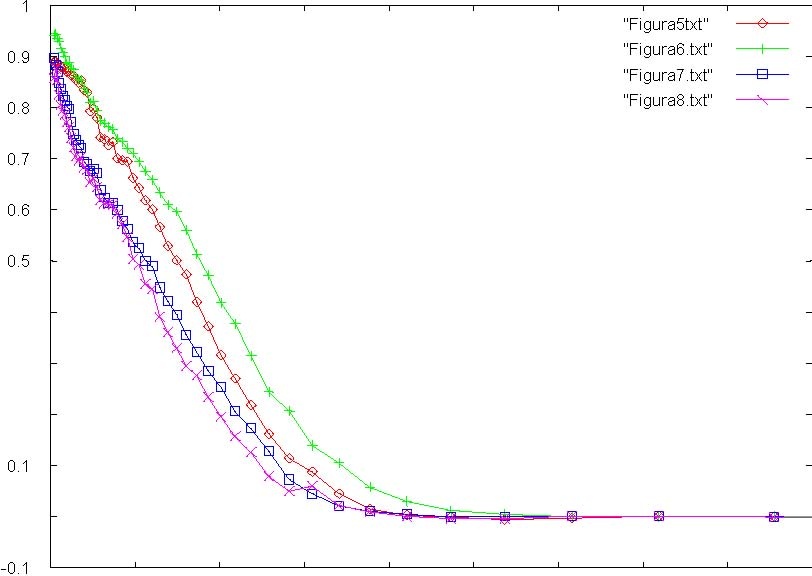
Figura 9: Gráficas MTF correspondientes a las figuras 5, 6, 7 y 8.
La resolución media que se obtiene para cada imagen se muestra en la siguiente tabla (vea Tabla 2):
|
Imagen |
Resolución (píxel) |
| Figura 5 | 0,83 |
| Figura 6 | 0,79 |
| Figura 7 | 1,07 |
| Figura 8 | 1,32 |
Tabla 2: Resolución media para cada imagen aérea.
En relación con dichos resultados, es importante señalar la relación entre la resolución media de la imagen y la curva MTF obtenida. Se observa una relación de proporción inversa entre el valor de resolución media y el área delimitada por la curva correspondiente. En efecto, una mayor área comprendida entre la curva MTF y el eje de abscisas indica una menor pérdida de contraste para cada frecuencia y eso se traduce en una mejor resolución de la imagen.
3.4 Validación de los algoritmos. Criterio de inspección visual
La validación de los algoritmos se ha realizado a partir de una fotografía capturada mediante cámara analógica y posteriormente escaneada a 7 y 14 micras de resolución. En ella aparece el patrón de Siemens anterior pintado sobre lona de 100 m2, y un patrón USAF (vea Figura 10).
Dado que la fotografía dispone de una serie de franjas de anchura y longitud variables, el criterio consiste en localizar el mínimo tamaño de franja que se puede resolver y comparar sus dimensiones con los resultados dados por el programa.
En el proceso de inspección visual se establece que la última capa del patrón USAF de la imagen escaneada a 7 micras no es distinguible, siendo su anchura de 6,3 cm. La resolución media que se obtiene mediante el algoritmo es 1,98 píxeles, que se traducen en 6.35 cm., puesto que las medidas reales de los patrones son conocidas. La aproximación visual y la medida calculada a partir del algoritmo difieren en 0,05 cm., un error absoluto considerablemente reducido.
Siguiendo la misma metodología para la imagen escaneada a 14 micras, se establece que la penúltima capa del patrón USAF no es distinguible, siendo su anchura 7 cm. La resolución media que se obtiene mediante el algoritmo es 1,08 píxeles, que se traducen en 6,94 cm. El error absoluto en este caso, 0,06 cm., también es reducido y muy similar al anterior.
3. Conclusiones
1) Se han desarrollado dos herramientas que nos proporcionan información sobre la capacidad resolutiva de un sistema y se ha comprobado, utilizando la Transformada de Fourier, que ambas son consistentes.
2) Se han generado medidas absolutas de resolución a partir de un patrón estrella de Siemens cuyas dimensiones son conocidas, y que parece especialmente indicado por el hecho de disponer de un elevado número de contornos que abarcan todo el rango angular.
3) La MTF proporciona información sobre la pérdida de contraste del sistema para todas y cada una de las frecuencias presentes en la imagen.
4) La medida FWHM que se extrae de la función LSF proporciona una cuantificación concreta de la resolución del sistema, coherente con las técnicas de cálculo de resolución mediante patrones USAF.
4. Referencias
- [1] Honkavaara, E., Jaakkola, J., Markelin, L., Becker, S., 2006 Evaluation of Resolving Power and MTF of DMC. In proceedings of ISPRS Comission I Symposium, Paris.
- [2] Becker, S., Haala, N., Reulke, R., 2005. Determination and Improvement of digital aerial images. International Archives of Photogrammetry and Remote Sensing, Vol. 33, pp. 45-´52
- [3] Coltman, J.W., 1954. The specification of image properties by response to sine wave input. Journal of the Optical Society of America, Vol. 44, No. 6, pp. 468-471.
- [4] Blonski, S. 2001. Spatial Resolution of IKONOS Pan. Images: Characterization Based on Edge Responses. In: 2001 High Spatial Resolution Commercial Imagery Workshop, 19-22nd March 2001, Greenbelt, MD (USA).
- [5] Blonski, S., Pagnutti, M., Ryan, R. E. and Zanoni, V., 2002. In-flight edge response measurements for high spatial- resolution remote sensing systems. In: W. L. Barnes (ed.), Proceedings of SPIE: Earth Observing Systems VII, Vol. 4814, pp. 317–326.
- [6] Jacobson, R.,E., Ray, S.,F, Attridge, G.G., Axford,.N.R., 2002. Manual de Fotografía. Teoría de la formación de la imagen, pp. 407-426.



