Several authors have proven that large format digital aerial cameras are not free of systematic errors in their virtual image space as it was initially expected (see Honkavaara et al., 2006a and 2006b, Alamús et al., 2005 and 2006, Cramer, 2007, Dorstel, 2007 and Madani and Shkolnikov, 2008). If such systematic errors are not properly modelled, the estimated exterior orientation can absorb propagated errors in the bundle adjustment together with the effects of other error sources like poor GPS/INS observations or insufficient ground control set up (see Alamús et al., 2005 and 2006, and Schroth, 2007). In order to handle these systematic errors in aerotriangulation, two approximations are analysed in this paper: i) using self-calibration parameters in any aerotriangulation, and, ii) using a calibration grid. Self calibration in bundle adjustment is a well known technique (Ebner, 1976, Grün, 1979), extensively used with analogue images. On the other hand (Dörstel, 2007) and (Madani and Shkolnikov, 2008) propose to determine a calibration grid in a special calibration flight and later compensate for the detected systematic error during the virtual image generation process in future projects. This would allow to continue with aerotriangulation and any further process without changing mathematical modelling in comercial software or hardware like digital photogrammetric stations. In this paper performance of both methods in aerotriangulation is analysed, and the impact of the systematic errors in the virtual image space in photogrammetric processes after aerotriangulation is discussed.
As ICC owns two DMC cameras since 2005, the analysis carried out in this paper is based on DMC data sets. Other cameras may have different performance and different distribution and magnitude of systematic errors in image space. Thus, some conclusions cannot be applied for such sensors.
DMC system description
The DMC camera simultaneously captures a high resolution panchromatic images of 13 824 x 7 680 pixels (across-track and along-track respectively) and four multi-spectral images (red, green blue and near infrared) of 3 072 x 2 048 pixels. The high resolution image is formed from the four images acquired with four inclined panchromatic high resolution camera heads with a focal length of 120 mm. Each of these camera heads is covering a quarter of the final image, called virtual image. The four low resolution multi-spectral images are acquired by four additional nadir looking camera heads with a focal length of 25 mm. The four images completely cover the virtual high resolution image. (See Hinz, 1999; Zeitler et al., 2002; Dörstel et al., 2003 for details.)
1. DATA SETS
All data sets are taken with the same camera (DMC01-0026) at a) different ground sampling distances (GSD) and b) different times. It is important to focus on these two parameters because the calibration/characterization must be independent on both flying height (GSD) and time in order to be valid also for different flight configurations in future projects.
1.1.1 Salou 60%x60: this data set was acquired on 12th of October 2007. The block consisted of 230 images distributed in 10 parallel and three transversal strips taken at a flight altitude of 900 m above ground level, which corresponds to a GSD of 9 cm, and with 60% endlap and 60% sidelap. 10 natural GCP and 230 orientations derived from GPS/INS data were used to aerotriangulate the block. Moreover, 40 well distributed natural check points were measured in the images.
1.1.2 Salou 60%x30%: this data set was acquired on 2nd of July 2007. The block consisted of 112 images distributed in five parallel and two transversal strips taken at a flight altitude of 900 m above ground level, which corresponds to a GSD of 9 cm, and with 60% endlap and 30% sidelap. 10 natural GCP and 112 orientations derived from GPS/INS data were used to aerotriangulate the block. Moreover, 40 well distributed natural check points were measured in the images. Notice that this data set covers the same area and uses the same GCP and check points than Salou 60%x60%.
1.1.3 Vilafranca 60%x60%: this data set was acquired on 29th of October 2007. The block consisted of 175 images distributed in five parallel and four transversal strips taken at a flight altitude of 900 m above ground level, which corresponds to a GSD of 9 cm, and with 60% endlap and 60% sidelap. Five natural GCP and 175 orientations derived from GPS/INS data were used to aerotriangulate the block. Moreover, 11 well distributed natural check points were measured in the images.
1.1.4 Cervera: this data set was acquired on 9th of August 2007. The block consisted of 123 images distributed in four parallel and two transversal strips taken at a flight altitude of 750 m above ground level, which corresponds to a GSD of 7.5 cm, and with 60% endlap and 30% sidelap. 12 natural GCP and 123 orientations derived from GPS/INS data were used to aerotriangulate the block. Moreover, seven well distributed natural check points were measured in the images.
1.1.5 MTN 190: (MTN stands for Mapa Topográfico Nacional – National Topographic Map, and the data set name refers to the National Topographic Map sheet number) this data set was acquired on 28th of June 2007. The block consisted of 595 images distributed in 10 parallel taken at a flight altitude of 2 200 m above ground level, which corresponds to a GSD of 22 cm, and with 60% endlap and 30% sidelap. Eight natural GCP and 595 orientations derived from GPS/INS data were used to aerotriangulate the block. Moreover, 11 well distributed natural check points were measured in the images.
1.1.6 MTN 302: this data set was acquired on 6 and 7th of May 2007. The block consisted of 767 images distributed in 13 parallel taken at a flight altitude of 2 200 m above ground level, which corresponds to a GSD of 22 cm, and with 60% endlap and 30% sidelap. 10 natural GCP and 767 orientations derived from GPS/INS data were used to aerotriangulate the block. Moreover, 15 well distributed natural check points were measured in the images.
1.1.7 MTN 303: this data set was acquired on 6 and 8th of May 2007. The block consisted of 642 images distributed in 13 parallel taken at a flight altitude of 2 200 m above ground level, which corresponds to a GSD of 22 cm, and with 60% endlap and 30% sidelap. 11 natural GCP and 642 orientations derived from GPS/INS data were used to aerotriangulate the block. Moreover, 15 well distributed natural check points were measured in the images.
2. METHOD
The method used in the analysis is divided into three steps:
1. grid calibration (or characterization of the virtual image space)
2. comparison of performance in aerotriangulation of both models
3. analysis of the effects of systematic errors in a single stereopair.
2.1 Calibration grid derivation
The calibration grid is derived from the Salou 60%x60% data set employing aerotriangulation with a large number of tie point observations (up to 151 622 image observations in 230 images). They are derived with Match-AT software from Inpho and correspond to 23 441 object points. By relaxing the a priori standard deviations of the image observations in a bundle adjustment without any self-calibration parameter the systematic errors in image space, together with effects of other error sources, are projected into the virtual image space. Then, the systematic errors can be seen as image residuals. The calibration/characterization grid is computed as the weighted (inverse of the distance) moving average of the image residuals in along- and across-track directions. The grid has 321×577 nodes corresponding to along-track and across-track directions respectively. Fig. 1 shows the results from a block adjustment using highly weighted GPS observations (2.5 cm, 1 ), lowly weighted image observations (6 μm, 1 ) and no self-calibration parameters. In the same way a second calibration grid is derived from the Vilafranca 60%x60% block (see fig. 2). The difference between the two calibration grids, shown in fig 3, prove that the two results are similar, but not identical, although the two blocks were flown with only 17 days time difference under very similar conditions.
2.2 Comparison in performance in AT
The seven data sets described in section 2 are analysed comparing the results at independent check points of three different bundle adjustment set ups: i) not using any model, ii) using self-calibration, and iii) using the calibration grid to compensate for systematic errors without self-calibration. All the other parameters and observations are not changed. The used self-calibration approach respects the special DMC design and enables self-calibration of each single camera head (see Alamús and Kornus, 2006). It employs four sets of 12 parameters, which are related to the four quarters of the DMC image acquired by four different high resolution DMC camera heads.
2.3 Effects of systematic error in a single stereopair
The data set used in this section is Vilafranca 60%x60%. For five consecutive models selected in the middle of the block object point coordinates were calculated in four different ways:
1. applying the rigorous model used in AT, but considering only the stereopair image observations
2. using stereopair image observations and the exterior orientation computed model by model
3. using stereopair image observations compensated for image systematic errors by the calibration grid derived in Salou 60%x60% and the exterior orientation computed in 2.
4. using stereopair image observations compensated for image systematic errors by the calibration grid derived in Vilafranca 60%x60% and the exterior orientation computed in 2.
The model by model calculation in 2. employs a separate adjustment for the five selected models based on a Cartesian three dimensional system (the same as later used in restitution) instead of the national net projection used in the global block adjustment. Fixing the object coordinates of all model tie points estimated in the global adjustment an exterior orientation is calculated, which absorbs most of the differences between the reference systems minimizing the residuals in the object space. With this exterior orientation all tie points observed in the respective stereopair are projected into object space and compared to the estimated coordinates of the global bundle block adjustment.
3. RESULTS AND DISCUSSION
In this section results of the investigations are discussed.
3.1 Calibration grid results
As described in section 3.1 two different calibration grids have been derived for the camera DMC026 from the two data sets Salou 60%x60% and Vilafranca 60%x60%. The respective systematic image residuals are shown in fig. 1 and fig. 2. Both patterns are similar but not identical, although both data sets were taken within a time span of 17 days only. The patterns have differences up to 1/10th of a pixel and their distribution in image space is not random as can be observed in fig. 3. This fact suggest that systematic image distortions are either not stable in time or it is not possible to isolate image distortion patterns from other error sources involved in the adjustment and propagated into the image space (using the method described above in section 3.1). The systematic pattern, shown in fig. 3, may affect in bundle adjustment in a different way from block to block.
3.2 Results in performance in AT
Table 1 shows the results for the seven data sets and the three investigated scenarios in AT: i) no self-calibration, ii) calibration grid and iii) self-calibration (4 sets of 12 parameters). The goal is to evaluate which approximation can better handle the systematic error in image space and its propagation in the block adjustment together with other errors sources. There are three parameters to focus on: GSD, time passed since the calibration flight and the approach used for modelling the systematic errors in the virtual image space.

Figure 1. Adjusted image residuals corresponding to the DMC026 systematic errors in virtual image computed in Block Salou 60%x60% (bottom left square represents the size of a 1×1µm2 at the scale of the image residuals)
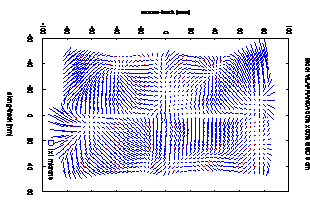
Figure 2. Adjusted image residuals corresponding to the DMC026 systematic errors in virtual image computed in Block Vilafranca 60%x60% (bottom left square represents the size of a 1×1µm2 at the scale of the image residuals)
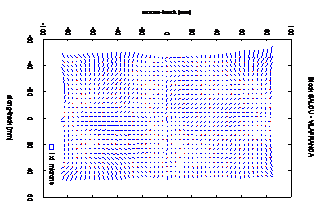
Figure 3. Difference of image residuals between Salou 60%x60% (fig. 1) and Vilafranca 60%x60% (fig. 2) data sets (bottom left square represents the size of a 1×1µm2 at the scale of the image residuals)
First of all, results using self-calibration show a small superiority compared to the calibration grid results for all data sets independent of flying time and flying altitude. This becomes even clearer in fig. 4, where the ratio of root-mean-squared (rms) height errors at the check points to the theoretical accuracy (0.05‰ of flying height according to (Dörstel, 2003)) along time is shown. Here the better performance is achieved with the self-calibration approach. By using this ratio, height accuracy is comparable independently of flying height. The results of the three adjustment set ups: not using any model, using a self-calibration parameter set and using the calibration grid compensation are plotted in red, bright green and dark blue respectively.
|
Block |
GSD |
time since calib. [d] |
No. CP | rms no ap [cm] |
rms grid [cm] |
rms |
|
|
Salou 60%x60% |
9.0 |
0 |
40 |
X | 9.9 | 4.9 | 2.4 |
|
|
Y |
10.3 |
6.0 |
2.3 |
|||
| h | 10.8 | 7.5 | 3.5 | ||||
|
Salou 60%x30% |
9.0 |
-71 | 40 | X | 3.2 | 3.0 | 3.2 |
| Y | 6.4 | 4.1 | 3.0 | ||||
| h | 6.0 | 6.9 | 4.8 | ||||
|
Vilafranca 60%x60% |
9.0 |
17 | 11 | X | 5.6 | 3.3 | 3.9 |
| Y | 7.7 | 4.0 | 3.7 | ||||
| h | 8.3 | 7.9 | 5.6 | ||||
|
Cervera 60%x30% |
7.5 |
-64 | 7 | X | 7.6 | 5.3 | 3.6 |
| Y | 10.8 | 8.0 | 4.2 | ||||
| h | 5.7 | 4.5 | 3.1 | ||||
|
MTN 190 60%x30% |
22.0 |
-106 | 11 | X | 12.0 | 11.1 | 10.0 |
| Y | 34.8 | 21.9 | 7.4 | ||||
| h | 16.9 | 15.3 | 14.8 | ||||
|
MTN 302 60%x30% |
22.0 |
-159 | 15 | X | 11.0 | 10.3 | 7.2 |
| Y | 21.9 | 35.7 | 8.0 | ||||
| h | 24.5 | 30.8 | 13.7 | ||||
|
MTN 303 60%x30% |
22.0 |
-158 | 15 | X | 12.9 | 12.9 | 6.8 |
| Y | 38.0 | 53.1 | 5.8 | ||||
| h | 34.6 | 43.8 | 12.3 |
Table 1. Rms height differences at check points (CP) for three different AT set ups: not using self-calibration (no ap), using calibration grid (grid) and using self-calibration (4 aps).
It is remarkable that for any of the data sets the use of self-calibration parameters is providing an rms in the level of the theoretical accuracy. The calibration grid solution always yields inferior solutions, which in two cases are even worse than the adjustment without modelling systematic errors at all. On the other hand there is a 22 cm GSD flight (4 months before calibration flight) where calibration grid compensation and self-calibration results are quite similar, which suggests that the calibration grid results may not that much be influenced by GSD or time dependent effects rather than by block configuration; in other words, results may be affected by error propagation of other sources in the adjustment like errors or uncertainties in GPS/INS and/or ground control observations).
3.3 Results in systematic error effects in a single stereopair
This subsection discusses the impact of systematic errors of virtual image space on the geometry of a single stereo pair with given exterior orientation The use of calibration grids, derived a) from a calibration flight and b) from the analysed block are compared against results obtained with the rigorous model and also without compensating for any systematic error in the virtual image at all.
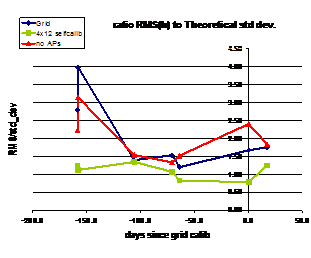
Figure 4. Ratio between the rms height differences dh at check points and the theoretical accuracy (0.05‰ of flying height) for three different AT set ups: not using self-calibration (no APs), using calibration grid (Grid) and using self-calibration (4×12 selfcalib).
Following the methodology described in subsection 3.3, the results are summarised in table 2. They show that i) there is not a significant improvement in using the calibration grid derived from the calibration flight or the calibration grid derived with the same data set under analysis, ii) using a calibration grid provides a solution in the same level of accuracy than the rigorous model used in bundle adjustment and iii) not using any systematic errors in image space model leads to an rms 1 cm worse (approximately 1/10th of GSD) than in the other three cases.
| Model |
rms |
rms |
rms |
rms |
|
| X | 1.3 | 2.0 | 1.6 | 1.5 | |
| 1 | Y | 2.7 | 3.3 | 2.7 | 2.6 |
| h | 5.5 | 6.9 | 5.7 | 5.4 | |
| X | 1.4 | 1.9 | 1.5 | 1.5 | |
| 2 | Y | 2.2 | 2.6 | 2.3 | 2.2 |
| h | 5.2 | 6.1 | 5.7 | 5.4 | |
| X | 1.2 | 1.8 | 1.4 | 1.4 | |
| 3 | Y | 3.7 | 3.5 | 3.1 | 3.0 |
| h | 7.1 | 7.3 | 6.3 | 6.2 | |
| X | 1.2 | 1.9 | 1.4 | 1.3 | |
| 4 | Y | 2.6 | 3.4 | 2.6 | 2.5 |
| h | 5.4 | 7.0 | 5.3 | 5.1 | |
| X | 1.2 | 2.0 | 1.5 | 1.5 | |
| 5 | Y | 2.0 | 2.8 | 1.9 | 2.0 |
| h | 4.2 | 6.3 | 4.6 | 4.8 |
Table 2. Rms at tie point object coordinates (compared against adjusted object coordinates in AT) in five different models using the rigorous model used in AT, a cartesian model without compensated tie points coordinates (w/o comp.), a cartesian model compensating image coordinates for Calibration grid computes used Salou 60%x60% data set (SG comp.) and a cartesian model compensating image coordinates for calibration grid computed in the same block: Vilafranca 60%x60% (VG comp.)
The performance of the four approximations has been evaluated using automatic derived tie points in aerotriangulation. The expected accuracy of such points is 1/10th of a pixel in image space. These results are not suitable to evaluate the impact of compensating for systematic image residuals whether image pointing accuracy were worse, as it is the case of a human operator instead of automatic derived points, than with the current data used in this analysis.
4. CONCLUSION
In this paper the performance of calibration grids (derived in a calibration flight and applied systematically in all data sets) in aerotriangulation is evaluated and compared to self-calibration in terms of their capacity to handle error propagation caused by non modelled systematic errors in the virtual image space. Although systematic errors in image space from two different calibration data sets show the same trends, the error patterns and, thus, the resulting calibration grids are different. This fact suggests that either the calibration grid is non-stable in time or that the method (presented in this paper) used to derive the calibration grid is not able to isolate image distortion patterns from errors of other sources involved in the bundle adjustment (e.g. GPS/INS, ground control, etc.).
In aerotriangulation, self-calibration results show a small superiority compared to calibration grid results, independently on flying height and on the time passed since the calibration flight. It has not been possible to prove stability in time of calibration grid compensation: it is not clear whether the poorer results are caused by temporal effects, by effects related to the flying altitude over the terrain or by other block configuration aspects.
In stereoplotting, calibration grid compensation for systematic errors in the virtual image leads to slightly improved accuracies.
The influence of systematic errors in the virtual image space is much more pronounced in bundle block adjustment than in stereoplotting or DSM processes, where the exterior orientation is given and non modelled error sources (in particular systematic errors in image space) are not propagated trough the block.
REFERENCES
- Alamús, R., Kornus, W., K., Palà, V., Pérez, F., Arbiol, R., Bonet, R., Costa, J., Hernandez, J., Marimon, J., Ortiz, M.A., Palma, E., Pla, M., Racero, S. and Talaya, J., 2005. Validation process of the ICC digital Camera. In: ISPRS Hannover workshop 2005 on High-Resolution Earth Imaging for Geospatial Information. 6 pages (on CD-ROM).
- Alamús, R., Kornus, W. and Talaya, J., 2006. Studies on DMC geometry. ISPRS Journal of Photogrammetry and Remote Sensing 60 (6): 375-386.
- Cramer, M., 2007. DMC User Forum, http://www.ifp.uni-stuttgart.de/eurosdr/Gaevle07-EuroSDR-DMC.pdf (accessed 1 March 2007).
- Dörstel, C., 2003. DMC- Practical Experiences and Photogrammetric System Performance. In: Photogrammetric Week 2003 (Ed. D. Fritsch). 292 pages: 59-65.
- Dörstel, C., 2007. DMC- (R)evolution on Geometric Accuracy. In: Photogrammetric Week 2007 (Ed. D. Fritsch). 350 pages: 81-88.
- Ebner, H., 1976. Self calibrating block adjustment. In: Bildmessung und Luftbildwessen, 44 (4): 128-139.
- Grün, A., 1979. Self-calibration versus Testfield calibration (Results from Jämijärvi, Willunga and Kapunda testfields). In: ISP Working group III/3. Aalborg /Denmark May 17-18. 24 pages.
- Hinz, A., 1999. The Z/I Digital Aerial Camera System. In: Photogrammetric Week 1999. (Eds. D. Fritsch and R. H. Spiller). 380 pages: 109-115.
- Honkavaara, E., Ahokas, E., Hyyppä, J., Jaakkola, J., Kaartinen, H., Kuittinen, R., Markelin, L. and Nurminen, K., 2006a. Geometric test field calibration of digital photogrammetric sensors. In: ISPRS Journal of Photogrammetry and Remote Sensing 60 (6): 387-399.
- Honkavaara, E., Jaakkola, J., Markelin, L. and Ahokas, E., 2006b. Theoretical and empirical evaluation of geometric performance of multi-head large format photogrammetric sensors. In: International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences 36 (1): 56-61. Also 6 pages (on CD-ROM).
- Madani, M. and Shkolnikov, I., 2008. Further investigation into geometric accuracy of DMC. In: International Calibration and Orientation Workshop EuroCOW 2008. 13 pages (on CD-ROM).
- Schroth, R.W., 2007. Large format digital cameras for aerial survey of geospatial information. In: FIG Working Week 2007. 15 pages (on CD-ROM).
- Zeitler, W., Dörstel, C. and Jacobsen, K., 2002. Geometric Calibration of the DMC: Method and Results. In: International Archives of Photogrammetry and Remote Sensing, 34 (1): 324-333. Also 6 pages (on CD-ROM).



