Abstract
The Mediterranean Sea is a semi-enclosed true ocean. Recent Mediterranean circulation and sea level studies using various observations and ocean general circulation models show good coherence and agreement. The satellite altimetry and tide gauge observed and model predicted sea level show good coherent with correlation coefficient of 0.6. The barotropic pressure response accounts for about 66% of the Mediterranean sea level rise (1948-2001). The estimated sea level trend (1.54 ± 0.75 mm/yr) using decadal altimetry (1985-2001) after correcting the interannual/decadal signals reconstructed using tide gauge data, agrees well with the long term trend (1948-2001) estimated using tide gauges (1.43 ± 0.09 mm/yr) in the Mediterranean Sea, and is in better agreement than before with the global long-term sea level trend (1.7 – 1.8 mm/yr). Simulation studies indicate that the time-varying mass variations of Mediterranean Sea likely are sensitive to GOCE at the few mEötvös level.
One of GOCE’s primary high-level data products is the global gravity model with anticipated geoid accuracy of 1 cm RMS and a spatial resolution of 130 km or longer.
Actually, the International Centre for Global Earth Models (ICGEM) distributes some GOCE’s Global Gravity field Models (GGMs) like GO_CONS_GCF_2_DIR (Bruinsma et al, 2010), GO_CONS_GCF_2_TIM (Pail et al, 2010a), GO_CONS_GCF_2_SPW (Migliaccio et al, 2010), GOCO01S (Pail et al, 2010b).
The work focuses on the comparison between these GOCE’s GGMs, EGM2008 and EIGEN-51C, with sea gravity anomalies and geoid undulations provided by existing local and regional geoids – like IBERGEO (Sevilla, 2008), IGG (Corchete et al, 2005), etc. – in the Western Mediterranean Sea in order to find the GGM that best fits this area.
We also try to estimate how the GOCE geoid data, provided by ESA, works on the Western Mediterranean Sea in order to prepare future geomatic issues.
Introduction
The main objective is the determination of the Mean Dynamic Topography from GOCE, altimetry, GPS and in situ tide gauges in the Western Mediterranean Sea. The combination of satellite gravity missions, GRACE and GOCE, is expected to make a significant contribution to improving the long-wavelength, satellite derived component of the gravitational field of the Earth.
The Western Mediterranean Sea is a quite complex area for different reasons: presence of several islands, coastal lines, shallow waters and a peculiar hydrologic equilibrium due to its proximity to the Atlantic water exchange area. This makes the estimation of the gravity field and the geoid slope quite a difficult task.
There are some results for the local/regional gravimetric geoid, which have been built up using different techniques such as least squares collocation (LSC) and spectral methodology as fast Fourier transform. In all cases, the classical remove-restore technique has been employed, taking into account the long wavelength part of the gravity field. The result is a fairly smooth surface.
Long-term (~100 years) sea level records in the form of tide gauge stations exist at the northern coasts of the Western Mediterranean basin at Marseille, Genova, Trieste and Venice, and a larger number of tide gauge records with 40-year data span exist.
The intention of this study is to present the behaviour of different Earth’s global gravity field models over the Western Mediterranean Sea.
ICGEM Models
To accomplish this study, it is importat that all the Earth’s global gravity field moldes have the same data format and available to the public as products of geodesy. These reasons are some of the objectives of the International Centre for Global Earth Models (ICGEM) that was established in 2003 as a one of six centres of the International Gravity Field Service (IGFS).
One of the ICGEM’s objectives is collecting and long-term archiving of existing global gravity field models and making them availablle on the web.
A web-interface to calculate gravity functionals from the spherical harmonic models on freely selectable grids, with respect to a reference system of the user’s choice, is provided. The following functionals are available: height anomaly, geoid height, gravity disturbance and gravity anomaly. Filtering is possible by selecting the range of used coefficients or the filter length of a Gaussian averaging filter.
In this paper some geoid models have been computed, the selected parameters of the calculation service used are defined in Table 1 and Table 2 shows the information about the ICGEM models used in this study.
| Parameter | Value |
| product_type | gravity_field |
| Shmname | model_file |
| max_used_degree | d/o |
| tide_system | tide_free (tf) / zero_tide (zt) / mean_tide (mt) |
| Functional | Geoid |
| zero_degree_term | Included |
| Unit | Meter |
| Refsysname | GRS80 |
| long_lat_unit | Degree |
| latlimit_north / south | 45.0 / 35.0 |
| long_limit_west / east | 0.0 / 10.0 |
| Gridstep | 0.05 |
| latitude/longitude_parallels | 201 / 201 |
| number_of_gridpoints | 40401 |
| Gapvalue | 999.0 |
| Gridformat | long_lat_value |
Table 1. ICGEM calculation service parameters used.
Differences of one model varying the parameter TIDE_SYSTEM
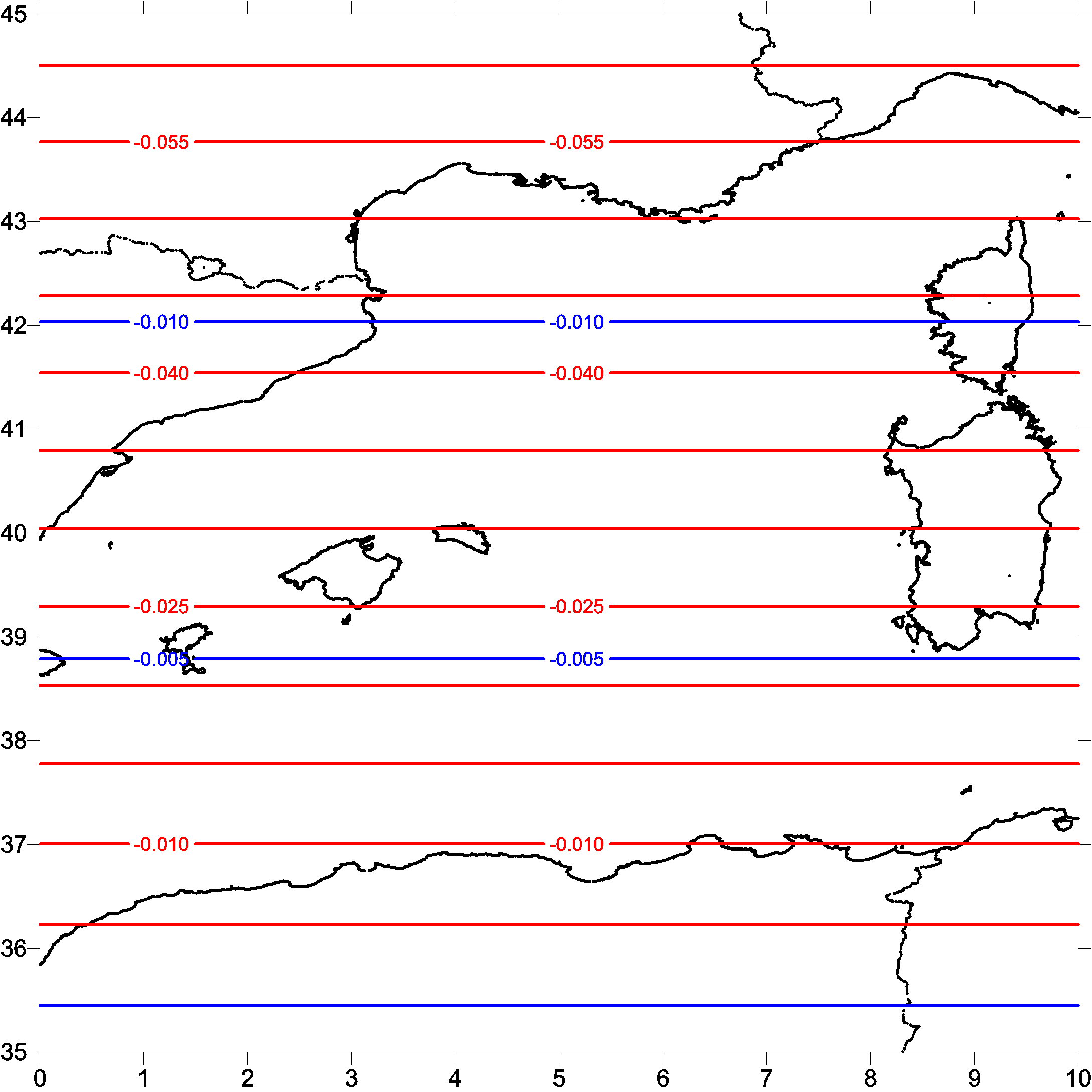
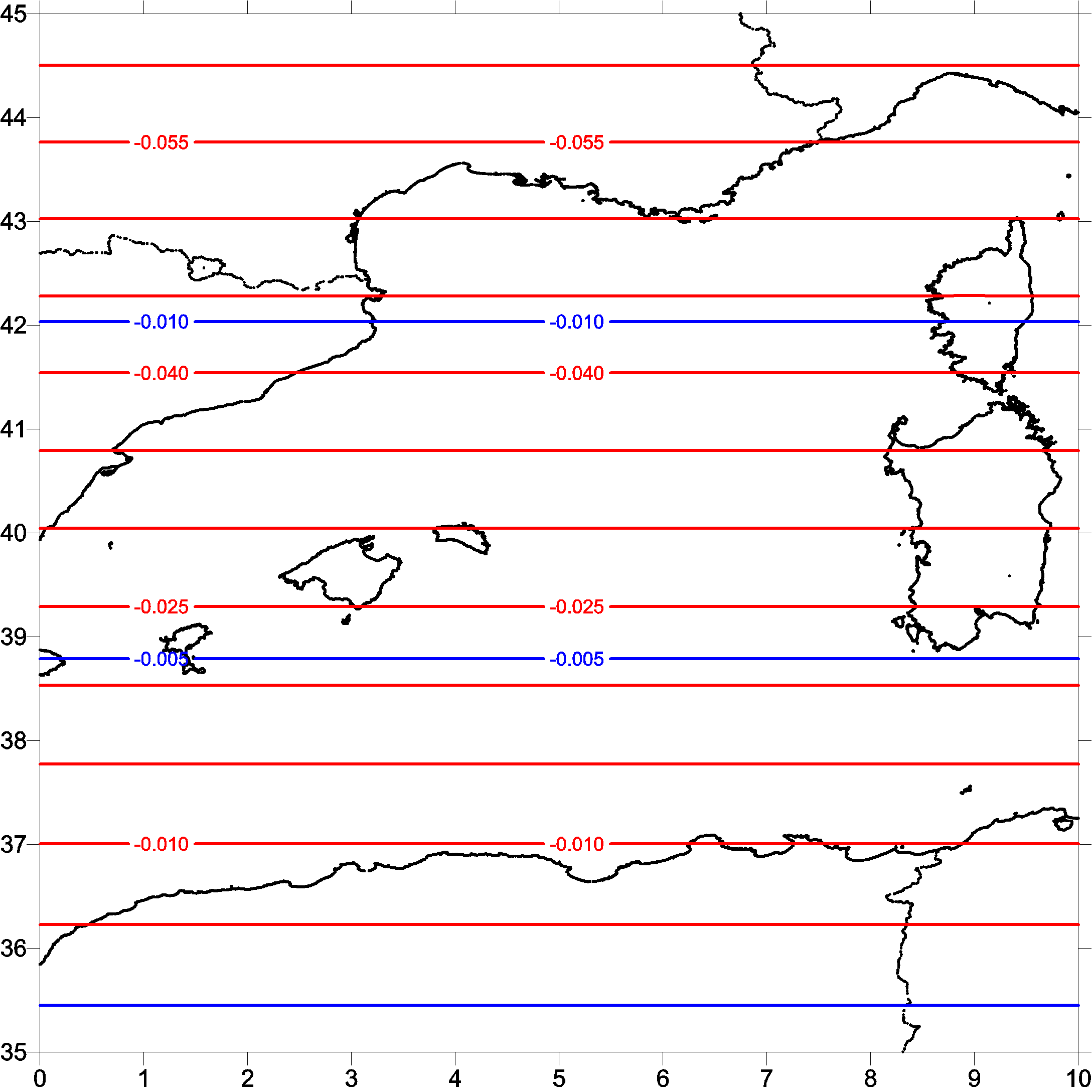
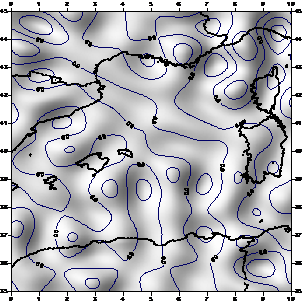
We start the study with the evaluation which type of tide system has to be used in the computations of this paper. Fig. 1, Fig. 2 and Fig. 3 shows the differences between zero_tide and mean_tide respect to tide_free system from the models egm2008, go_cons_gcf_2_tim_r2 and go_cons_gcf_2_dir_r2, respectively.
|
|
model_file |
d/o |
Data |
|
01 |
egm2008 |
2190 |
S(GRACE),G,A |
|
02 |
egm2008upto360 |
360 |
S(GRACE),G,A |
|
03 |
Itg-grace2010s |
180 |
S(GRACE) |
|
04 |
eigen-champ05s |
150 |
S(CHAMP) |
|
05 |
eigen-51c |
359 |
S(GRACE), S(CHAMP),G,A |
|
06 |
goco01s |
224 |
S(GOCE) |
|
07 |
Go_cons_gcf_2_spw_r1 |
210 |
S(GOCE) |
|
08 |
Go_cons_gcf_2_tim_r1 |
224 |
S(GOCE) |
|
09 |
go_cons_gcf_2_dir_r1 |
240 |
S(GOCE) |
|
10 |
go_cons_gcf_2_tim_r2 |
250 |
S(GOCE) |
|
11 |
go_cons_gcf_2_dir_r2 |
240 |
S(GOCE) |
Table 2. ICGEM Earth global gravity models.
After the analysis of these differences -only an offset- all the models in this study have been computed using tide free system.
 |
 |
|
Figure 1. Differences of egm2008 model varying the tide system. |
Figure 2. Differences of go_cons_gcf_2_tim_r2 model varying the tide system. |
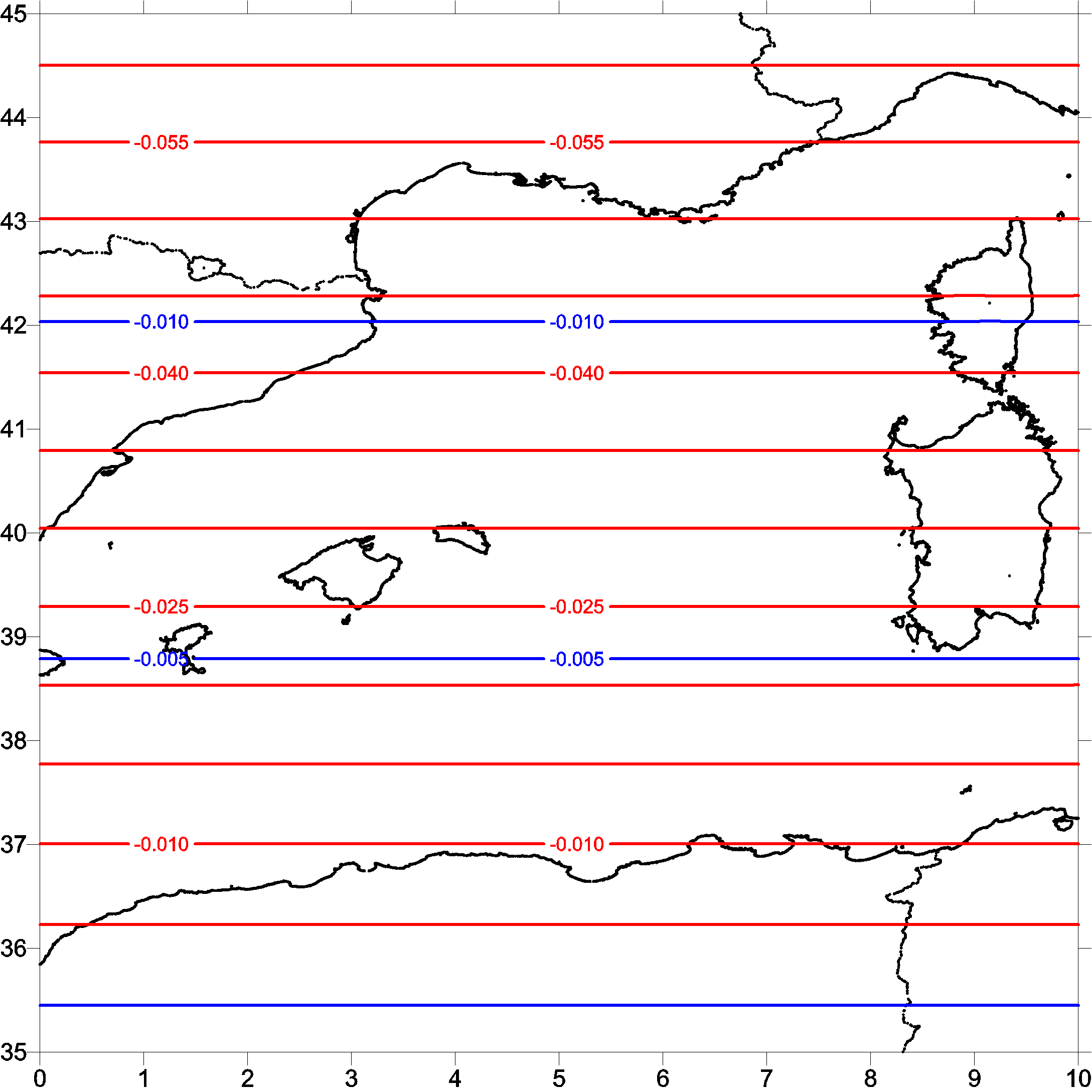
Figure 3. Differences of go_cons_gcf_2_dir_r2 model varying the tide system.
Red lines: mean_tide vs tide_free. Blue lines: zero_tide vs tide_free.
Differences of one model varying the parameter TIDE_SYSTEM
In this section, we have computed the differences between these 3 models, taking as reference the egm2008 model. Remember that all the models are computing using the tide_free system.
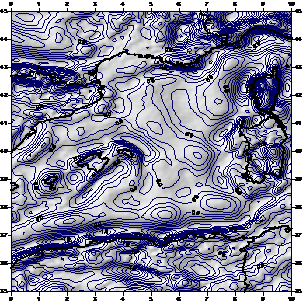
Fig. 5, Fig. 6 and Fig. 7 shows the differences of the GOCE models, go_cons_gcf_2_tim_r2 and go_cons_gcf_3_dir _r2 respectivelly, respect the egm2008 model.
 |
 |
|
Figure 4. Differences between eigen-51c and egm2008. |
Figure 5. Differences between go_cons_gcf_2_tim_r2 and egm2008. |
 |
 |
|
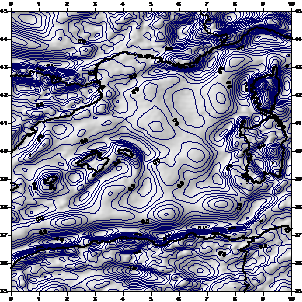
Figure 6. Differences between go_cons_gcf_2_dir_r2 and egm2008. |
Figure 7. Differences between go_cons_gcf_2_tim_r2 |
At the moment of writing this paper, the authors are evaluating the differences between each two models listed in Table 2. The statistics of this evaluation are shown in Table 3.
|
Dat |
grd | Min | Mean | Max | Std |
| 01 | 05 | -1.041 | 0.000 | 1.384 | 0.248 |
| 01 | 10 | -1.564 | 0.005 | 2.574 | 0.444 |
| 01 | 11 | -1.538 | -0.003 | 2.457 | 0.445 |
| 10 | 11 | -0.492 | -0.008 | 0.376 | 0.116 |
Table 3. Statisticals of the residuals of two geoid models, computed as N(residuals)=N(dat)-interpol(N(grd)).
GPS/Levelling Comparison in Tide Gauge Stations
It is also interesting to evaluate independent data, as GPS/levelling, existing on the area. We start with tide gauge stations where exist GPS and levelling measures.
Fig. 8 shows the Spanish tide gauge network REDMAR.
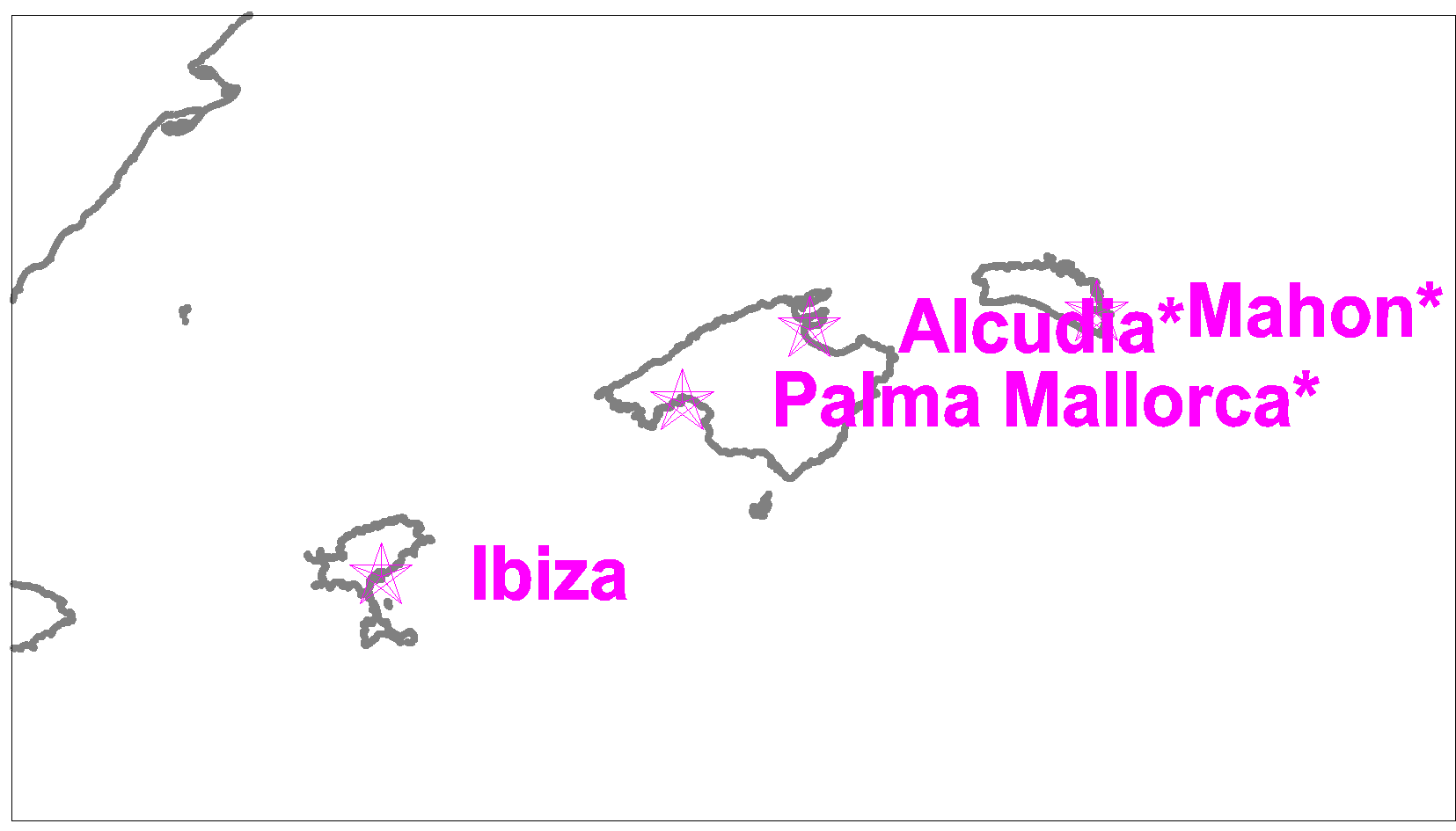
Figure 8. REDMAR network of tide gauges in Spain over the Western Mediterranean Sea.
Despite that all the existing tide gauges (Barcelona, Sagunto, Valencia, Gandia, Mahó, Alcudia, Palma, Ibiza and Formentera) in the Western Mediterranean Sea has been levelled, only the tide gauges of Palma de Mallorca and Ibiza has also GPS data.
Every tide gauge has different height zero reference (Fig. 9) which are used for different purposes: NMMA , mean sea level of the tide gauge (ZP), and the hidrographic zero (ZH).
We need more GPS/levelling data in order to obtain some conclusions. But the authors have a good feeling about the good results which can be obtained from GOCE models.
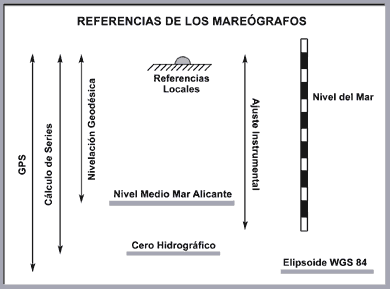
Figure 9. Relation between the different height references in a tide gauge.
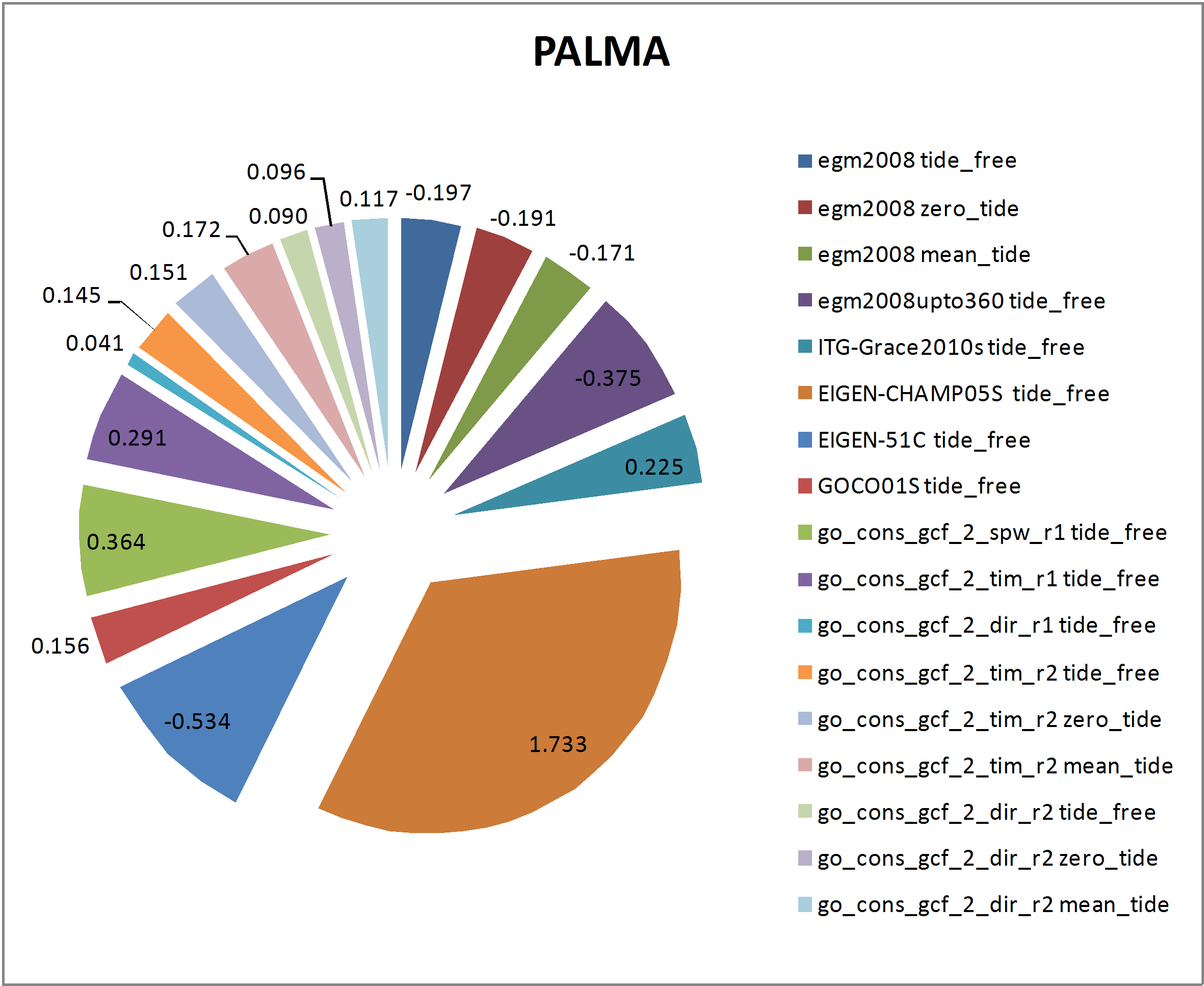
Figure 10. Residuals of geoid ondulations in Palma tide gauge.
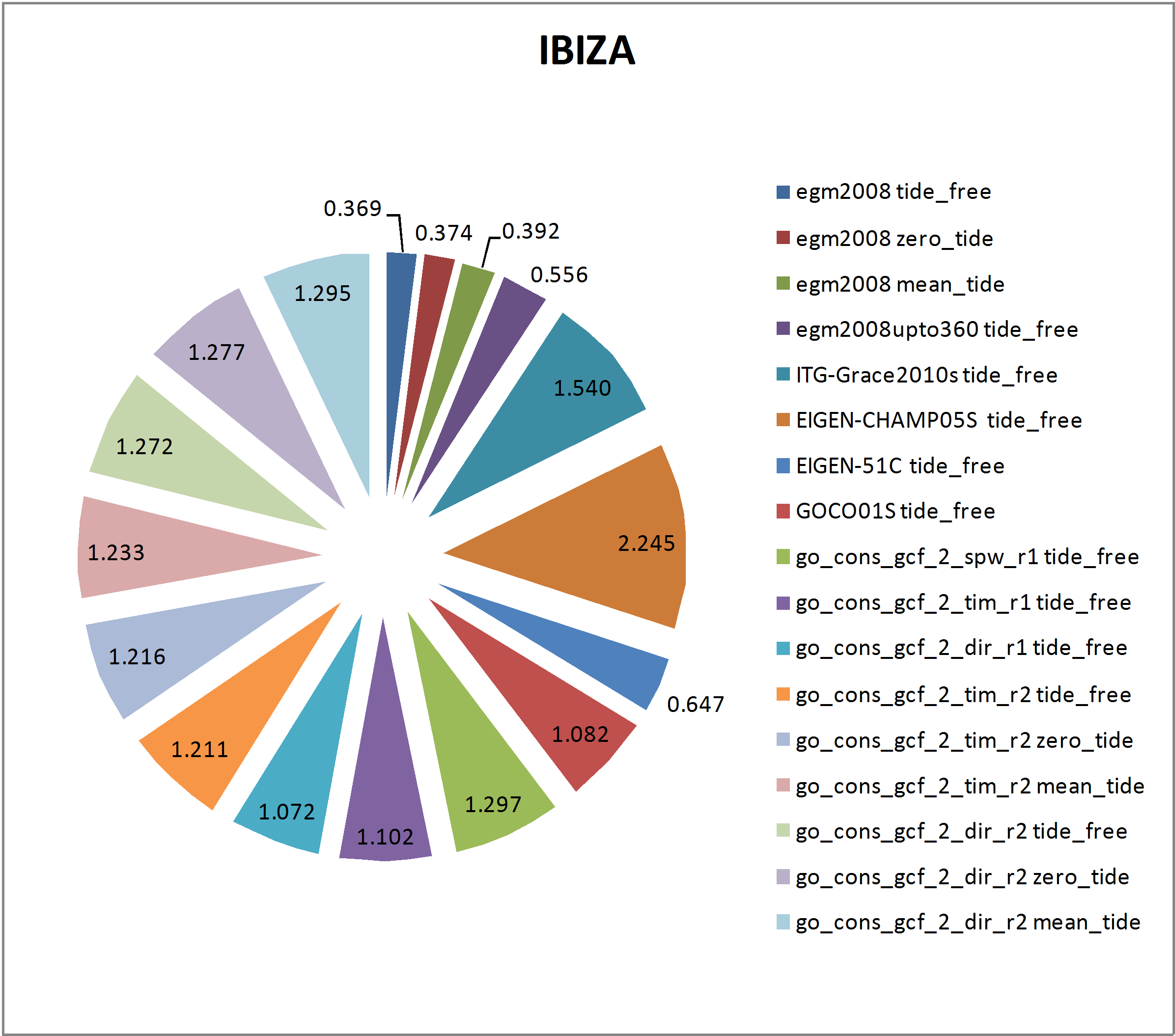
Figure 11. Residuals of geoid ondulations in Ibiza tide gauge.
Conclusions
The evaluations of this paper are a first approximation to the work that has to be done in the area.
The authors believe that the combined models that will be obtained in the next future – some EGMyyyy with GRACE and GOCE – will improve the results of this first evaluation.
The evaluation can be also complete with the computation of residuals of more GPS/levelling in land.
This work has been done inside the framework of the MICINN project: CGL2008-05244-E.
References
- Bruinsma et al, 2010. GOCE Gravity Field Recovery by Means of the Direct Numerical Method.
- ESA AO.GOCE.4312. “Calibration/Validation of GOCE data products in the Mediterranean Sea”.
- Flechtner et al, 2010. The Release 04 CHAMP and GRACE EIGEN Gravity Field Models.
- GOCO consortium, 2010. Combined satellite gravity field model GOCO01S derived from GOCE and GRACE.
- Mayer-Gürr et al, 2010. ITG-Grace2010 Gravity Field Model.
- Migliaccio et al, 2010. GOCE data analysis: the space-wise approach and the first space-wise gravity field model.
- Pail et al, 2010. GOCE gravity field model derived from orbit and gradiometry data applying the time-wise method.
- Pavlis et al, 2008. An Earth Gravitational Model to Degree 2160: EGM2008.



