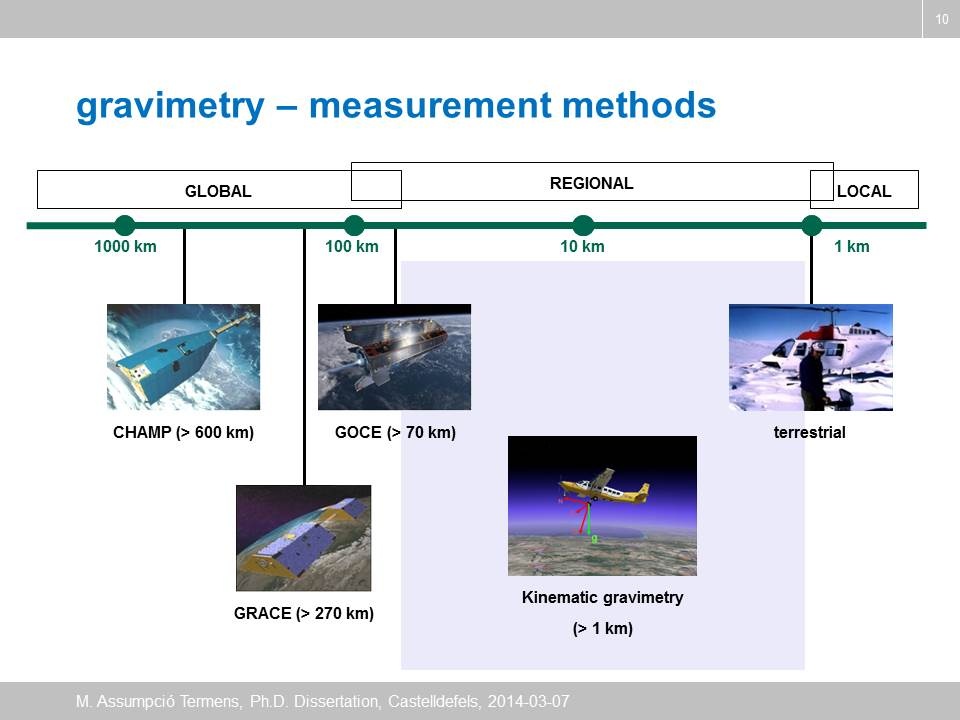
The determination of the Earth’s gravity field is one of the most important areas in geodesy for the determination of the geoid and for the prediction of dynamical parameters of low Earth-orbiting satellites. In addition, gravity information is important for many scientific and engineering areas such as geophysical exploration and navigation, and in studying geophysical phenomena of the Earth. Traditionally, the gravity signal is determined by measuring its magnitude with a gravimeter and the deflections of the vertical, defined by the difference of the directions between the natural gravity and normal gravity vector, by astronomical observations. Although this produces highly accurate gravity vector information, it is extremely expensive and time consuming.
Due to recent satellite technology, it is possible to determine the gravity field using satellite observations, mostly in the form of satellite altimetry. Now there are available different refined global gravity models based on terrestrial gravity and satellite data, e.g. EGM2008 or EIGEN. Hence the long wavelength gravity signal can be obtained by using a global model. However, the shorter-wavelength signatures of the global model are either poorly modelled or only moderately well known in the global model.
The purpose of aerial gravimetry is to recover the Earth’s gravity field on the medium-frequency gravity signal, which then fills the gap between the terrestrial gravity field measurements and global gravity models in the wavelengths between 1 and 100–200 km.
Geoid resolution by measurement wavelengths.
Measurements from CHAMP, GRACE and GOCE provide revolutionary improvements in our knowledge of the Earth’s static gravity field and its temporal component. Especially, the accuracy of the mean geoid -by GOCE- is about 1 cm at a wavelength of 100 km or longer. The accuracy and resolution from these missions, however, are still not good enough for geophysical exploration in which 1 mGal over less than 10 km is required. In addition, there are polar gaps with radius of 700 km due to the sun-synchronised orbits for GOCE. Therefore, even after these missions, airborne gravimetry still plays an important role improving the Earth’s gravity field modelling.
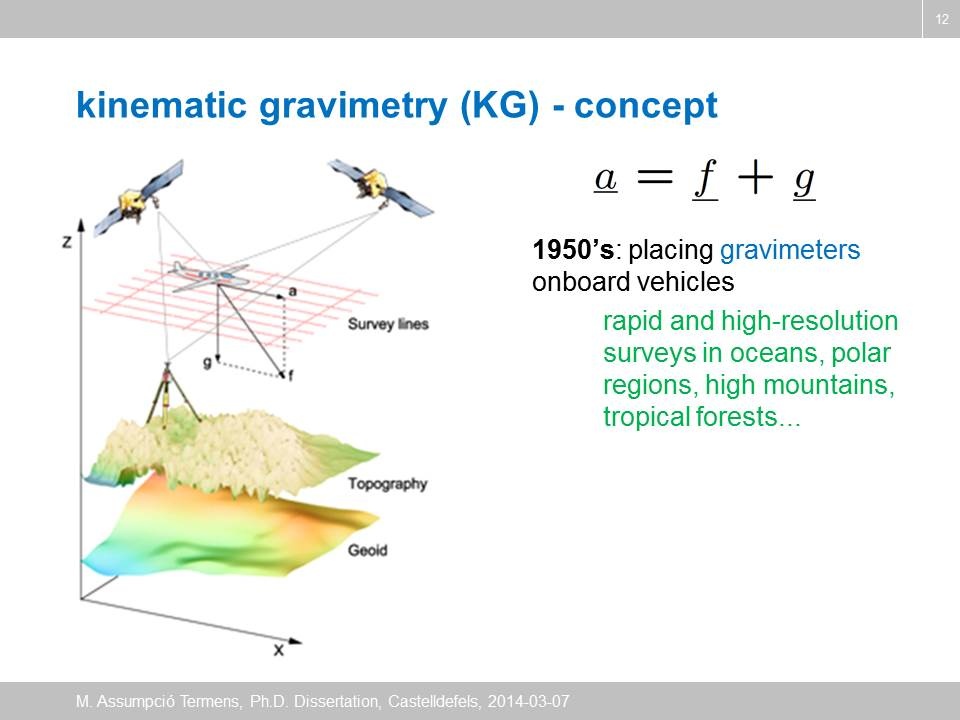
As a matter of fact, the Inertial Navigation System (INS) was introduced as a surveying instrument in the late 1960’s, and immediately it was noticed that the potential of INS for precise positioning was limited by the unknown anomalous gravity field.
Principiple of airborne gravimetry (Source: TUDelft).
Conversely, this means that the anomalous 3D gravity field could be recovered from the INS instrument if accurate kinematic positions and/or velocities were known and the system errors were kept small.
The important issue in gravity recovery using INS is the separation of the gravitational acceleration from kinematic acceleration as well as from instrumental errors. The kinematic acceleration can be separated from the sensed acceleration of INS by using a different sensor such as GPS. The separation between the gravitational acceleration and system errors from INS can be achieved by introducing external information, e.g. ZUPT (Zero Velocity Update Point).
Obviously, an alternative way of determining the kinematic position and velocity was necessary to perform mobile, especially airborne, gravity surveys. Moritz proposed in 1967 ([1]) the combination of INS and a gravity gradiometer, and simulation studies on such a combination showed promising results. Because of the high cost of the gradiometers, however, other combinations such as the combination of INS with a radio navigation system, LORAN-C, were investigated.
Clearly, the advent of the Global Positioning System (GPS), providing high accuracy position and velocity, created revolutionary progress in the area of airborne gravimetry. At that time, Schwarz ([2]) compared different kinematic methods for airborne gravimetry with combinations of GPS, INS and gradiometers.
Compared to the other positioning instruments, GPS is inexpensive and the accuracy of the vehicle acceleration from GPS is generally sufficient for airborne gravimetry.
INS/GPS gravimetry is mainly affected by two error sources: short term GPS-derived acceleration errors and long term INS inertial sensor errors ([3]). For geoid determination applications, short term errors (i.e., the noise of GPS-derived accelerations) have been identified as one of the limiting factors of the technique. Fortunately, the situation will likely improve significantly with the GPS modernisation programme and the advent of the European global navigation satellite system Galileo, because of its higher signal-to-noise ratio and with the subsequent use of hybrid Galileo/GPS receivers.
The correct measurement of gravity with INS/GPS gravimetry depends on the correct separation of the INS/GPS errors from the actual variations of the gravity field itself. This separation is, in principle, feasible because of the different characteristics of the two signals: errors of the inertial sensors can be reasonably modelled as time functions, whereas the variations of the gravity field are, strictly, spatial functions. An improvement of the calibration of inertial sensors may be seen as an improvement of the long wavelength errors of INS/GPS gravimetry. By doing so, we are not only achieving an overall improvement of INS/GPS gravimetry but, in particular, we are extending its spectral window of applicability. This extension might be instrumental to the integrated use of GOCE gravimetry and INS/GPS gravimetry as the sole means of gravimetry for geoid determination.
There have been various studies on the feasibility of INS/GPS gravimetry in both time and spectral domains. This research has shown that the gravity disturbance can be recovered with errors, defined by wavelengths, in the order of (RMS) ±1-2 mGal using a high-accuracy INS within a spectral window of 10-200 km.
The main challenge in INS/GPS gravimetry is the low signal to noise ratio of the system. Typically, the gravity disturbance vector does not exceed 100 mGal in each component over distances of about 100 km, while the noise level of the system is much higher. Analysis and simulations were conducted by many investigators, mainly applying a low pass filter on the signal to reduce the system noises and extract the optimal gravity signatures in INS/GPS airborne gravimetry. In addition, the development as well as the analysis of the INS error model has been investigated theoretically, and tested throughout simulations. Recently, some test flights have been also carried out to determine the feasibility and to assess the accuracy in airborne gravimetry. It has been shown that 1 mGal accuracy in GPS acceleration and 2-3 mGal of accuracy in the vertical gravity component can be achieved.
Problem statement and objectives
There are two main techniques in airborne gravimetry based on accelerometer measurements, namely scalar gravimetry and vector gravimetry. Gravity gradiometry may be considered as the third type, where the observations are gradients of gravity. Scalar gravimetry determines either the vertical component or the magnitude of the gravity anomaly vector while vector gravimetry aims at recovering the full gravity anomaly vector in all three dimensions.
Currently, airborne gravimetry is conducted using either sea/air gravimeters on a Schuler-tuned stabilised platform for scalar gravimetry, or with an Inertial Navigation System -mainly strapdown INS and we will refer to it as INS/GPS gravimetry- for scalar or vector gravimetry. In both cases, the separation of the gravitational and kinematic accelerations from the system errors is crucial in estimating the gravity field. Results of scalar airborne gravity survey using gravimeters, modified for the higher dynamics of the aircraft, in Greenland, Antarctica and Switzerland show that an accuracy of 3-5 mGal and a resolution of 10 km wavelength is achievable with current technology. The main error source in these cases was insufficient platform stabilisation. Another test using the ITC-2 inertial platform system showed that an accuracy of 1 mGal with resolution of 2-3 km is achievable.
Unlike the stabilised systems, there is no physical stabilising platform in a strapdown system. Instead, the inertial sensors are physically bolted down to the vehicle so that the measured data in the IMU instrumental (know as body) frame are transformed to the local level frame or ECEF frame (e-frame) computationally. The advantage of the strapdown INS is its smaller size, lower cost and more operational flexibility. It has been shown that the performance of the INS/GPS systems is comparable to that of the airborne gravimeter([4],[5]).
The traditional way of analyzing the determination of gravity using the INS/GPS signal is to integrate the error dynamic equations or the dynamic equations of the INS system, and model the gravity disturbance and the INS errors as stochastic processes. The a priori stochastic information of the INS errors, such as biases and scale factors, are obtained from the manufacturer’s specifications and from further extensive and tricky calibration and field testing based modelling.
Remember that a dynamical system can be considered to be a rule for time evolution on a state space. The above described method is known as State-space Approach (SSA) and it is an optimal procedure for real-time applications. But this method cannot use all the existing observational information contained in a survey because it has a serious disadvantage trying to deal with space correlations -measurements involving states at different times. A good example of this limited capacity is the difficulty of a rigorous treatment of crossover points.
The key to overcome such limitations is to look at the system as stochastic differential equations (SDE) that, through discretisation, leads to a geodetic network widely used in geodesy, photogrammetry and remote sensing. The discretisation of dynamic observation models together with static (auxiliary) observation models and further network least-squares adjustment will be referred to as the Network Approach (NA).
There are two basic objectives in this dissertation:
- prove the feasibility of the NA for the rigorous determination of the gravity field using INS/GPS techniques;
- to show that the above use of NA methodology shall provide, within the essential limitations of the technology, a procedure to simultaneously calibrate the INS sensors and estimate the anomalous gravity field.
There is a central idea in this dissertation: the use of the Network Approach allows the use of information -observations- that the State-space Approach cannot take, thus facilitating the achievement of the two above objectives.
Thesis Outline
One of the main objectives of this research is to investigate algorithms to better calibrate the systematic errors of the inertial sensors. More specifically, the research of an alternative geodetic procedure to the traditional Kalman filtering and smoothing borrowed from navigation. The advantage of the new procedure is that it can assimilate all the information available in a gravimetric (aerial) mission; from ground gravity control to the crossover or multiple-flight-line conditions, among other observational information types. The proposed procedure is nothing else than geodesy as usual in that we redefine the INS/GPS gravimetry problem as a network adjustment problem. In a more general perspective, the use of the NA procedure as a genuine geodetic method for non real-time navigation and positioning problems has been proposed in [6] and [7].
This thesis is divided as follows:
- Chapter 2 reviews the concept of airborne gravimetry.
- Chapter 3 covers the concept of the NA method. In this chapter, the dynamic and static observation models that can be assimilated by the NA for INS/GPS gravimetry are reviewed. Their implantation in the ICC GeoTeX/ACX program is described. As well, some implementation issues of NA are discussed: limitations found and future improvements.
- Chapters 4 and 5 present the experimental results of the NA concept. The experiments use INS simulated data and demonstrate that the proposed NA procedure works.
- Chapter 6 summarises the main contributions of this study and provides suggestions and recommendations for further research.
Concluding Remarks
Despite of the simple stochastic error models used, the main objectives of the research have been met. In the following, more detailed comments are made about the above contributions and improvements resulting from the research. Important results are highlighted, conclusions are drawn and recommendations are given.
Specific contributions:
• It has been demonstrated that the NA approach allows the use of information -observations- that the SSA cannot take and facilitating the achievement of the two above objectives. The development of an adjustment method in genuinely geodetic post-process, with the explicit purpose to determine precise gravity anomalies taking advantage at maximum the space characteristics of the gravitational field, has been validated with simulated data and configurations.
• It has been also demonstrated that gravity determination is considerably improved when additional observation models (DGUPT, GDT and XOVER) are taken into account. These models are related to previous knowledge of the gravity field that SSA approach can not handle with.
• Several implementations of the same observation equation have been considered depending on the parameters. At this moment, gravity parameters can be computed directly as gravity disturbance vector expressed in ECEF-frame, expressed in NED-frame or as gravity and deflections of the vertical. The gravity parameters, that have been computed in all the adjustments described in Chapter 4 are expressed as (g,η,ζ)T, where g is the gravity and (η,ζ) are the deflections of the vertical and later transformed into NED-framed gravity vector using Equation (C.20).
• The INS mechanisation equations and additional observation equations studied in this research have been implemented into the existing GeoTeX system of the ICC (the GeoTeX/ACX program), which is used since 1988 for both research and production projects.
• With GeoTeX/ACX development, different number of IMU and GNSS data can be managed at the same time. As a consequence, it is possible to validate one sensor from the knowledge of another one.
• The NA approach used in this dissertation (random walk stochastic error models) works properly for tactical-grade IMU sensors. It has been proved by the LN200 data.
Recommendations:
• The NA approach works properly for small networks and simulated data. However this work should continue with the validation using real data. This goal is highly related with the improvements of computer hardware technology, and with further research of numerical and geodetic methods to handle large amount of data and also to increase the redundancy of the resulting network.
• In the future, many modelling and estimation problems in geomatics may benefit from the concept of time dependent network. All the research that is now being carried on in this direction promise to obtain better results than the ones presented here.
• In this dissertation, the INS mechanisation equations in e-frame have been considered. It could be interesting to study the network adjustment if the NED-frame mechanisations are implemented. The same reasoning will be done for the parameters. Now position is expressed in cartesian coordinates and quaternions are used to express the attitude parameters. Consequently, the development of the observation equations with geodetic coordinates and with roll, pitch and heading angles should be studied.
• In spite of the fact that all the gravity data computed in Chapter 4 are expressed as (g,η,ζ)T, where g is the gravity and (η,ζ) are the deflections of the vertical, they have not been studied in depth. As mentioned before, g is transformed later into NED-framed gravity vector using Equation (C.20) and used in the results analysis.
With respect to usually applied gravimetric techniques for geoid computation, the deflections of the vertical (η,ζ) -usually astrogeodetically determined- represent an independent complementary data set that can be used for validation purposes and combined computations. So, further research work about vertical deflection data determination can be done.
• It is recommended to fully exploit the statistical and geometric information that the NA provides like covariances, correlations, redundancy numbers, etc. In this dissertation, it has not been studied in depth, but further research work should be done.
• The random walk stochastic error model for gravity data has to be improved. Further studies using Gauss-Markov models of different order and other stochastic models have to be carried out to investigate gravity models based on stochastic differential equations that are symmetric with respect to time as opposed to the Gauss-Markov model. This is a work for one o more dissertations (or Ph.D. thesis).
• It is recommended to continue the research on IMU error modeling as done since long by various groups.
• GeoTeX/ACX software is able to handle with different types of IMU and GNSS data jointly. Thus, it is possible to study and to determine (i.e calibrate) an IMU error model through the knowledge of another IMU model. Although this IMU calibration has not been studied in this dissertation, it is recommended to perform further research work about it.
References
- [1] Moritz,H. (1967). Kinematical Geodesy. Report N.92, Department of Geodetic Science and Surveying, Ohio State University, Columbus.
- [2] Schwarz,K.P. (1987). Approaches to Kinematic Geodesy. In: Geodetic Theory and Methodology. Publ.N.60006. Department of Surveying Engineering, University of Calgary.
- [3] Schwarz,K.P., Li,Y.C. (1995). What can airborne gravimetry contribute to geoid determination? Airborne Gravimetry, IAG Symposia G4, IUGG XXI General Assembly, Boulder, Colorado, pp.143-152.
- [4] Glennie,C., Schwarz,K.P. (1999). A comparison and analysis of airborne gravimetry results from two strapdown inertial/DGPS systems. Journal of Geodesy, 73:311-321.
- [5] Glennie,C., Schwarz,K.P., Bruton,A.M., Forsberg,R., Olesen,A.V., Keller,K. (1999). A comparison of stable platform and strapdown airborne gravimetry. IAG General Assembly, July 19-30 1999, Birmingham, UK.
- [6] Colomina,I., Blázquez,M. (2004). A unified approach to static and dynamic modelling in photogrammetry and remote sensing. ISPRS International Archives at Photogrammetry, Remote Sensing and Spatial Information Sciences, Vol.35-B1, Comm.I, pp.178-183.
- [7] Colomina,I., Blázquez,M. (2005). On the stochastic modeling and solution of time dependent networks. Geomatics Week, Barcelona.


